Версия 1.1.2
Релиз посвящен работе с популярными финансовыми коэффициентами. Обновление доступно через pip.
Коэффициент Сортино
- метод
get_sortiono_ratio() доступен в классах AssetList и Portfolio
Коэффициент Сортино является аналогом Коэффициента Шарпа. Разница в том, что в знаменателе учитывается не волатильность а полуотклонение (среднеквадратичное отклонение ниже целевой доходности, downside deviation):
S = \frac{R_p-R_t}{DR}
R_p - матожидание доходности портфеля (среднее арифметическое доходности)
R_t - целевая доходность портфеля
DR - полутоклонение доходности
Пример сравнения Коэффициента Сортино для различных активов:
al = ok.AssetList(['VOO.US', 'BND.US'], last_date='2021-12')
al.get_sortino_ratio(t_return=0.03) # целевая доходность равна 3%
VOO.US 1.321951
BND.US 0.028969
Коэффициент Сортино для инвестиционного портфеля:
pf = ok.Portfolio(['VOO.US', 'BND.US'], last_date='2021-12')
pf.get_sortino_ratio(t_return=0.02)
1.4377728903230174
Коэффициент диверсификации
Коэффициент диверсификации показывает на сколько эффективно применяется корреляция для снижения риска в портфеле. В отличие от коэффициентов Шарпа и Сортино в формуле не используется доходность. Речь идет только о снижении риска:
DR(w) = \frac{\sum_{i=1}^{N} w_i \times \sigma_i}{\sigma}
w_i - вес ценной бумаги в портфеле
\sigma_i - риск (среднеквадратическое отклонение) доходности ценной бумаги
\sigma - риск инвестиционного портфеля
Из формулы хорошо видно, что коэффициент диверсификации (КД) всегда больше единицы. Взвешенная сумма рисков активов всегда больше или равна риску портфеля.
Чем больше КД, тем выше снижен риск за счет низкой корреляции.
- атрибут
diversification_ratio доступен для Portfolio
- оптимизации по КД возможна в классе EfficientFrontier через метод
get_most_diversified_portfolio(). Метод позволяет получить как глобальный оптимизированный портфель, где КД достигает максимальной величины, так и локально оптимизированный портфель для заданной доходности портфеля.
- множество оптимизированных по КД портфелей доступно через атрибут
mdp_points в EfficientFrontier. Оптимизация происходит последовательно для промеж
Преимущество оптимизированных по КД портфелей заключается в том, что в отличие от Границы эффективности в них нет “вырожденных” весов. Поэтому для конструирования реальных инвестиционных портфелей распределение по КД - это хорошая подсказка.
ВНИМАНИЕ: использовать в явном виде эти веса нельзя, так же как и веса портфелей на Границе эффективности.
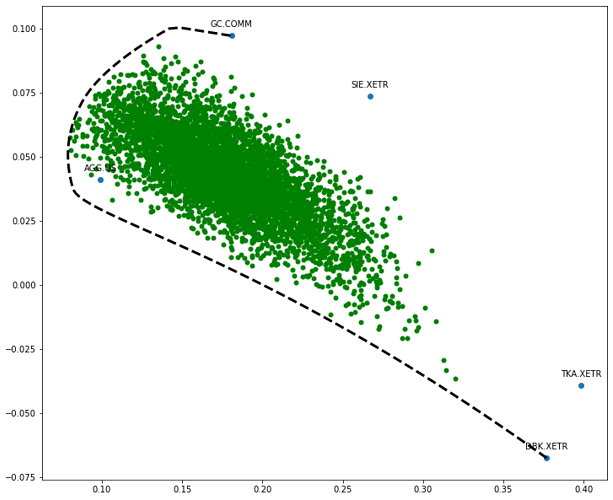
Пример построения кривой максимально диверсифицированных портфелей и Границы эффективности. В примере использованы портфели, составленные из:
- Индекс S&P500 полной доходности (SP500TR.INDEX)
- Индекс Мосбиржи полной доходности (MCFTR.INDEX)
- Индекс облигаций федерального займа Мосбиржи (RGBITR.INDX)
- Спотовые цены на золото (GC.COMM)
ls4 = ['SP500TR.INDX', 'MCFTR.INDX', 'RGBITR.INDX', 'GC.COMM']
y = ok.EfficientFrontier(assets=ls4, ccy='RUB', n_points=100)
# n_points=100 задает количество точек на Границе эффективности и на кривой
# максимально диверсифицированных портфелей
mdp = y.get_most_diversified_portfolio() # Глобальный максимально диверсифицированный портфель
mdp
{'SP500TR.INDX': 0.18734372897034768,
'MCFTR.INDX': 0.023902608406034215,
'RGBITR.INDX': 0.6595979466663215,
'GC.COMM': 0.12915571595729658,
'Mean return': 0.12279521203933563,
'CAGR': 0.12124953230039481,
'Risk': 0.059120398386235534,
'Diversification ratio': 1.9671253973462728}
df = y.mdp_points # множество локально оптимизированных по КД портфелей (100 шт)
ef = y.ef_points # портфели на Границе эффективности (100 шт)
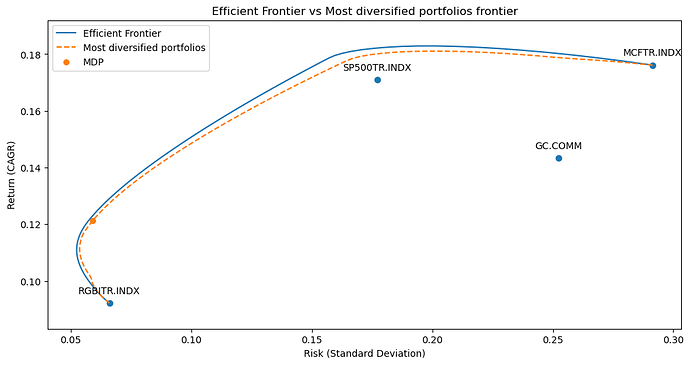
Строим графики Границы эффективности, Кривой максимально диверсифицированных портфелей, отображаем точку, где КД максимален:
fig = plt.figure()
# Отображение точек риск-доходность для каждой ценной бумаги
y.plot_assets(kind='cagr') # kind should be set to "cagr" as we take "CAGR" column from the ef_points.
ax = plt.gca()
# Отображение Границы эффективности
ax.plot(ef['Risk'], ef['CAGR'], label='Efficient Frontier') # на оси Y мы отображаем среднегодовую доходность (CAGR)
# Отображение кривой с максимально диверсифицированными портфелями
ax.plot(df['Risk'], df['CAGR'], linestyle='dashed', label='Most diversified portfolios')
# Отображение точки с максимальным КД (глобальный максимум). Обозначен как MDP
ax.scatter(mdp['Risk'], mdp['CAGR'], s=30, marker='o', label='MDP')
# Название графика и надписи осей
ax.set_title('Efficient Frontier vs Most diversified portfolios frontier')
ax.set_xlabel('Risk (Standard Deviation)')
ax.set_ylabel('Return (CAGR)')
ax.legend();